Funkcja Użyteczności

Mapa Obojętności

• Zbiór krzywych obojętności nazywany mapą obojętności.
• Pokazuje stopy substytucji między dwoma towarami dla każdego poziomu ich bieżącej konsumpcji.
• Im wyżej położona krzywa obojętności, tym wyższy poziom satysfakcji z zakupu dóbr.
• Wyraża upodobania konsumentów.

Dobra Doskonałe Substytuty

• Użyteczności dóbr będących doskonałymi substytutami są takie same.
• Mogą być wymieniane w stosunku 1:1.
• Nachylenie wynosi
  
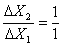
• Relacja zastępowalności jest zawsze taka sama, bez względu na proporcje konsumpcji.

Punkt Równowagi Konsumenta

• Wyznaczamy rozwiązując układ równań:
  • Funkcja użyteczności: (U = X_1 + X_2)
  • Ograniczenie budżetowe: (m = p_1 X_1 + p_2 X_2)

Dobra Doskonałe Komplementarne

• Konsumowane w równych proporcjach.
• Zmiana konsumpcji tylko jednego dobra nie zmienia użyteczności.
• Funkcja użyteczności: (X_1 = X_2)
• Ograniczenie budżetowe: (p_1 X_1 + p_2 X_2 = m)

Zastępowalność Dóbr

• Istnieje wzajemna zastępowalność dóbr (X_1) i (X_2), ale nie są to doskonałe substytuty ani dobra doskonałe komplementarne.
• Nachylenie krzywych obojętności równe relacji cen
  

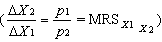
Ogólna Charakterystyka Funkcji Użyteczności

• Rozpatrywana jako funkcja dwóch zmiennych, choć może mieć dowolną liczbę zmiennych.
• Obrazem funkcji jest krzywa obojętności, określająca kombinacje koszyków dóbr o tej samej użyteczności.

Krótkookresowa Stopa Substytucji (MRS)

• Ilość jednego dobra, jaką konsument jest skłonny oddać za dodatkową jednostkę drugiego dobra.
• Zawsze malejąca, co świadczy o wypukłej krzywej obojętności.

Funkcje Użyteczności

1. Doskonałe Substytuty

• (U = X_1 + X_2)
• Równowaga konsumenta przedstawiona graficznie.

2. Doskonałe Komplementarne

• (U = \min{X_1, X_2})
• Równowaga konsumenta przedstawiona graficznie.

3. Funkcja Użyteczności Cobb-Douglasa

• Specyficzna forma funkcji użyteczności.
• Równowaga konsumenta wyznaczana przy pomocy funkcji Lagrange'a:
  
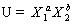
• Pochodne cząstkowe funkcji (L) przyrównywane do zera.